Esto que parece sacado del fondo del mar es una figura geométrica llamada plano hiperbólico. Y resulta que entre una hoja de papel y un plano hiperbólico, sería éste el que más se asemeja al espacio tal cual es.
Vamos explicando. Según los axiomas de la geometría euclidiana, esa que nos enseñaron en el colegio, por un punto exterior a una línea recta se puede trazar una sola recta paralela. Todas las demás líneas intersectarán a la primera en algún momento. Pues bien, en una superficie plana calza todo perfecto. ¿Pero qué pasa si se aplica ese axioma a una esfera, por ejemplo?

En una superficie curva las líneas rectas no se verán derechas, sino (duh) curvas. Estas líneas reciben el nombre de geodésicas y se definen como el camino más corto entre dos puntos. En una esfera este camino corto siempre es un»gran círculo», un círculo que divide a la esfera en dos hemisferios. Al dibujar un punto fuera de una geodésica inevitablemente la geodésica que tracemos en él cortará a la otra.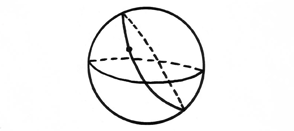
Si en la superficie plana teníamos una línea que nunca tocaba a la otra, ahora hay una superficie distinta donde no existe ninguna. Durante muchos años los matemáticos intentaron resolver esta inquietud, hasta que llegaron a la conclusión de que estaban mirando mal. Porque el espacio no se trata de un plano recto como las hojas de papel en las que hacían sus cálculos, sino de una superficie que puede ser vista desde muchas perspectivas. En este espacio no es una la recta que es paralela a otra. Son muchas. Tantas que decidieron llamarlo espacio hiperbólico.

Esas líneas no parecen rectas, pero recordemos que las de la esfera tampoco, a pesar de que sí lo son. Aquí es donde (finalmente) entra el crochet. En 1997, la matemática Daina Taimina tejió a crochet su primer modelo de un plano hiperbólico.
Este modelo permite observar y tocar las características del plano hiperbólico, que a medida que se extiende en el espacio van apareciendo en sus bordes intrincadas curvas. Además sirve para examinar facilmente el comportamiento de las líneas rectas o geodésicas y demostrar la falsedad del postulado de las líneas paralelas.

Estos modelos son geniales. Se puede leer mucho sobre geometría y creer que se entiende, pero una vez que tienen un pedazo de espacio en la mano se comprende todo. O incluso pueden llegar a algunas conclusiones sin tener idea de axiomas y teorías. Tejan su propio plano hiperbólico, bórdenle algunas líneas rectas y ya verán lo que les digo. En la página del Institute for Figuring encontrarán más información, pero en inglés.

INSTRUCCIONES:
Usen acrílico tieso y gordo, ese que no comprarían para ningún otro proyecto, así queda más firme. Los planos hiperbólicos se construyen siguiendo un índice de aumentos N. Por ejemplo, un N=4 quiere decir que se debe hacer un aumento cada cuatro puntos. Mientras menor sea el valor N, más corrugado será el modelo.
Base: Teje una fila de cadenetas de 20 puntos.
Fila 1: Haz una cadeneta, teje tres puntos bajos, teje dos puntos bajos en el siguiente punto de la base. Repite hasta el final y da vuelta.
Fila 2 y siguientes: igual que la primera.

Ustedes pueden escoger el índice de aumento que deseen. También pueden tejer circularmente, haciendo una anilla en lugar de una fila de cadenetas. Jugando con estas variables y usando distintos tipos de lanas, pueden crear algo como esto.

Imágenes y gráficos:
Quoin
Institute for Figuring